Der Algorithmus von Dijkstra (nach seinem Erfinder Edsger W. Dijkstra) dient der Berechnung eines kürzesten Pfades zwischen einem Startknoten und einem beliebigen Knoten in einem kantengewichteten Graphen. Die Gewichte dürfen dabei nicht negativ sein. Für Graphen mit negativen Gewichten aber ohne negative Zyklen ist der Bellman-Ford-Algorithmus geeignet.

Für nicht zusammenhängende, ungerichtete Graphen kann der Abstand zu bestimmten Knoten auch unendlich sein, wenn ein Pfad zwischen Startknoten und diesen Knoten nicht existiert. Dasselbe gilt auch für gerichtete, nicht stark zusammenhängende Graphen.

Inhaltsverzeichnis

1 Algorithmus
2 Grundlegende Konzepte und Verwandtschaften
3 Berechnung eines Spannbaumes
4 Zeitkomplexität
5 Anwendungen
6 Siehe auch
7 Literatur
8 Weblinks
9 Literatur / Literature
10 Weblinks
11 Code

Algorithmus

G bezeichnet den gewichteten Graphen mit V (engl. vertex) als Knotenmenge, E (engl. edge) als Kantenmenge und Kosten als Gewichtsfunktion. s ist der Startknoten, U (engl. unvisited) ist die Menge der noch zu bearbeitenden Knoten und z ist ggf. ein spezieller Zielknoten, bei dem abgebrochen werden kann, wenn seine Distanz zum Startknoten bekannt ist.

Nach Ende des Algorithmus enthält Distanz die Abstände aller Knoten zu s. In Vorgänger ist ein spannender Baum der von s aus ausgehenden minimalen Wege in Form eines In-Tree gespeichert.

Wird bei Erreichen von z abgebrochen (mit #optional gekennzeichet), so enthalten Distanz und Vorgänger diese Werte nur für alle zuvor betrachteten Knoten. Dies sind mindestens die, die kleineren Abstand als z zu s besitzen.

01  für jedes v aus V
02      Distanz(v) := unendlich, Vorgänger(v) := kein
03  Distanz(s) := 0, Vorgänger(s) := 'begin', U := V
04  M := EMPTYSET 
05  für jedes (s,v) aus E mit v aus U
06      Distanz(v) := Kosten(s,v) 
07      M := M UNION {v}
08      Vorgänger(v) := s
09
10  solange M nicht leer
11      wähle u aus M mit Distanz(u) minimal                               
12      M := M - {u}  
13      U := U - {u}                                              
14      wenn u = z dann STOP   # optional
15      für jedes (u,v) aus E mit v aus U
16          M := M UNION {v} 
17          wenn Distanz(u) + Kosten(u,v) < Distanz(v) dann
18              Distanz(v) := Distanz(u) + Kosten(u,v)
19              Vorgänger(v) := u

Grundlegende Konzepte und Verwandtschaften

Der Algorithmus gehört zur Klasse der Greedy-Algorithmen. Sukzessive wird der nächstbeste Knoten, der einen kürzesten Pfad besitzt (Zeile 06), in eine Ergebnismenge aufgenommen und aus der Menge der noch zu bearbeitenden Knoten entfernt (Zeile 07). Damit findet sich eine Verwandtschaft zur Breitensuche, die ebenfalls solch ein gieriges Verhalten aufweist.

Ein alternativer Algorithmus zur Suche kürzester Pfade, der sich dagegen auf das Optimalitätsprinzip von Bellman stützt, ist der Floyd-Warshall-Algorithmus. Das Optimalitätsprinzip besagt, dass, wenn der kürzeste Pfad von A nach C über B führt, der Teilpfad A B auch der kürzeste Pfad von A nach B sein muss.

Ein weiterer alternativer Algorithmus ist der A*-Algorithmus, der den Algorithmus von Dijkstra um eine Abschätzfunktion erweitert. Falls diese gewisse Eigenschaften erfüllt, kann damit der kürzeste Pfad unter Umständen schneller gefunden werden.

Berechnung eines Spannbaumes

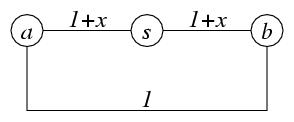
Negative Kante sorgt für Unklarheiten bei Knoten a

Nach Ende des Algorithmus ist in Vorgänger ein spannender Baum der Komponente von s aus kürzesten Pfaden von s zu allen Knoten der Komponente verzeichnet. Dieser Baum ist jedoch nicht notwendigerweise auch minimal, wie die Abbildung zeigt:

Sei x eine Zahl größer 0. Minimal spannende Bäume sind entweder durch die Kanten {a,s} und {a,b} oder {b,s} und {a,b) gegeben. Die Gesamtkosten eines minimal spannenden Baumes betragen 2+x. Dijkstras Algorithmus liefert mit Startpunkt s die Kanten {a,s} und {b,s} als Ergebnis. Die Gesamtkosten dieses spannenden Baumes betragen 2+2x.

Die Berechnung eines minimalen Spannbaumes ist mit dem Algorithmus von Prim oder dem Algorithmus von Kruskal möglich.

Zeitkomplexität

Im Folgenden sei m die Anzahl der Kanten und n die Anzahl der Knoten. Der Algorithmus von Dijkstra muss n mal den nächsten minimalen Knoten u bestimmen (Zeilen 05 und 06). Eine Möglichkeit wäre jedes Mal diesen mittels Durchlaufen durch eine Knotenliste zu bestimmen. Die Laufzeit beträgt dann <math>O(n^2)</math>. Eine effizientere Möglichkeit zur Liste bietet die Verwendung der Datenstruktur Fibonacci-Heap. Die Laufzeit beträgt dann lediglich <math>O(m+n\cdot\log (n))</math>.

Anwendungen

Routenplaner sind ein prominentes Beispiel, bei dem dieser Algorithmus eingesetzt werden kann. Der Graph repräsentiert hier das Straßennetz, welches verschiedene Punkte miteinander verbindet. Gesucht ist die kürzeste Route zwischen zwei Punkten.

Dijkstras Algorithmus wird auch im Internet als Routing-Algorithmus in OSPF eingesetzt.

Siehe auch

Literatur

E. W. Dijkstra: A note on two problems in connexion with graphs. In: Numerische Mathematik. 1 (1959), S. 269–271

Weblinks

Literatur / Literature

E. W. Dijkstra: A note on two problems in connexion with graphs. In: Numerische Mathematik. 1 (1959), S. 269–271
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0262032937. Section 24.3: Dijkstra's algorithm, pp.595–601.

Weblinks

Code

Implementations in various programming languages of Dijkstra's algorithm.

C

 void dodijkstra(int sr,int ds,int path[])
 {
         struct node
 	{
 	  int pre;   /* Predecessor */
 	  int length; /* Length between the nodes */
 	  enum {perm,tent} label; /* Enumeration for permanent and tentative labels */
 	}state[MAX];
 
 	int i,k,min;
 	struct node *p;
 	/* Initialisation of the nodes aka First step of Dijkstra Algo */
 	for(p=&state[0];p<&state[no_nodes];p++)
 	{
            p->pre= -1;
 	   p->length=INFTY;
 	   p->label=tent;
 	}
 	state[ds].length=0; /* Destination length set to zero */
 	state[ds].label=perm; /* Destination set to be the permanent node */
 	k=ds; /* initial working node */
 	/* Checking for a better path from the node k ? */
 	do
 	{
            for(i=0;i<no_nodes;i++)
 	      {
 		  if(dist[k][i]!=0 && state[i].label==tent)
 		     {
 			if((state[k].length+dist[k][i])<state[i].length)
 			   {
 			       state[i].pre=k;
 			       state[i].length=state[k].length+dist[k][i];
 		           }
 		     }
 	      }
              k=0;
              min=INFTY;
 	      /* Find a node which is tentatively labeled and with minimum label */
 	      for(i=0;i<no_nodes;i++)
 	      {
 		 if(state[i].label==tent && state[i].length<min)
 		    {
 			min=state[i].length;
 			k=i;
 		    }
 	      }
 	      state[k].label=perm;
 	} while(k!=sr);
 
 	i=0;
 	k=sr;
 	/* Print the path to the output array */
 	do {path[i++]=k;k=state[k].pre;} while(k>=0);
 	path[i]=k;
 }

C++

 #include < map>
 #include <queue>
 using namespace std;
 
 #define X first
 #define Y second
 
 template <class Node, class Edge=int> class Dijkstra {
    public:
    Dijkstra() {}
    Dijkstra(const Node &n, const Edge &e=0) { push(n, e); }
    bool empty() const { return q.empty(); }
    void push(const Node &n, const Edge &e=0) {
       Iter it = m.find(n);
       if (it == m.end()) it = m.insert(make_pair(n, e)).X;
       else if (it->Y > e) it->Y = e;
       else return;
       q.push(make_pair(e, it));
    }
    const Node &pop() {
       cur = q.top().Y;
       do q.pop();
       while (!q.empty() && q.top().Y->Y < q.top().X);
       return cur->X;
    }
    const Edge &dist() const { return cur->Y; }
    void link(const Node &n, const Edge &e=1) { push(n, cur->Y + e); }
 
    private:
    typedef typename map<Node, Edge>::iterator Iter;
    typedef pair<Edge, Iter> Value;
    struct Rank : public binary_function<Value, Value, bool> {
       bool operator()(const Value& x, const Value& y) const {
          return x.X > y.X;
       }
    };
    map<Node, Edge> m;
    priority_queue<Value, vector<Value>, Rank> q;
    Iter cur;
 };
 
 // Example usage (nodes and edges are represented with ints)
 int shortestDistance(int nodes, int startNode, int endNode, int **dists) {
    Dijkstra<int> dijkstra(startNode);
    while (!dijkstra.empty()) {
       int curNode = dijkstra.pop();
       if (curNode == endNode)
          return dijkstra.dist();
       for (int i = 0; i < nodes; i++)
          if (dists[curNode][i] >= 0) // "i" is a neighbor of curNode
             dijkstra.link(i, dists[curNode][i]); // add weighted edge
    }
    return -1; // No path found
 }

Actionscript

 class Dijkstra {	
 
 private var visited:Array;
 private var distance:Array;
 private var previousNode:Array;
 private var startNode:Number;
 private var map:Array;
 private var infiniteDistance:Number;
 private var numberOfNodes:Number;
 private var bestPath:Number;
 private var nodesLeft:Array;
 
 public function Dijkstra(ourMap:Array, startNode:Number, infiniteD:Number) {
     this.infiniteDistance = infiniteD;
     this.startNode = startNode;
     this.distance = new Array();
     this.previousNode = new Array();
     this.visited = new Array();
     this.map = ourMap;
     this.numberOfNodes = this.map[0].length;
     this.bestPath = 0;
     this.nodesLeft = new Array();
 }
 
 private function findShortestPath():Void {
     for (var i = 0; i < this.numberOfNodes; i++) {
          if (i == this.startNode) {
               this.visited[i] = 1;
               this.distance[i] = 0;
          }
          else {
               this.visited[i] = 0;
               this.distance[i] = this.map[this.startNode][i];
          }
          this.previousNode[i] = 0;
     }	
     while(this.somethingLeft(this.visited)) {
          this.nodesLeft = this.nodesNotVisited(this.visited);
          this.bestPath = this.findBestPath(this.distance, this.nodesLeft);
          this.updateDistanceAndPrevious(this.bestPath);
          this.visited[this.bestPath] = 1;
     }	
     this.getResults();
 }
 
 private function somethingLeft(ourVisited:Array):Boolean {
     for (var i = 0; i < this.numberOfNodes; i++) {
          if (!(ourVisited[i])) {
               return true;
          }
     }
     return false;
 }
 
 private function nodesNotVisited(ourVisited:Array):Array {
     var selectedArray = new Array();
     for (var i = 0; i < this.numberOfNodes; i++) {
          if (!(ourVisited[i])) {
               selectedArray.push(i);
          }
     }
     return selectedArray;
 }
 
 private function findBestPath(ourDistance:Array, ourNodesLeft:Array):Number {
     var bestPath = this.infiniteDistance;
     var bestNode = 0;
     for (var i = 0; i < ourNodesLeft.length; i++) {
          if (ourDistance[ourNodesLeft[i]] < bestPath) {
               bestPath = ourDistance[ourNodesLeft[i]];
               bestNode = ourNodesLeft[i];
          }
     }
     return bestNode;
 }
 
 private function updateDistanceAndPrevious(ourBestPath:Number):Void {
     for (var i = 0; i < this.numberOfNodes; i++) {
          if (!(this.map[ourBestPath][i] == this.infiniteDistance) || (this.map[ourBestPath][i] == 0)) {
               if ((this.distance[ourBestPath] + this.map[ourBestPath][i]) < this.distance[i]) {
                    this.distance[i] = this.distance[ourBestPath] + this.map[ourBestPath][i];
                    this.previousNode[i] = ourBestPath;
               }
          }
     }
 }
 
 private function getResults():Void {
     var ourShortestPath = new Array();
          for (var i = 0; i < this.numberOfNodes; i++) {
               ourShortestPath[i] = new Array();
               var endNode = null;
               var currNode = i;
               ourShortestPath[i].push(i);
               while(endNode != this.startNode) {
                    ourShortestPath[i].push(this.previousNode[currNode]);
                    endNode = this.previousNode[currNode];
                    currNode = this.previousNode[currNode];
               }
               ourShortestPath[i].reverse();
               trace("---------------------------------------");
               trace("The shortest distance from the startNode: "+this.startNode+
                     ", to node "+i+": is -> "+this.distance[i]);
               trace("The shortest path from the startNode: "+this.startNode+
                     ", to node "+i+": is -> "+ourShortestPath[i]);
               trace("---------------------------------------");
          }
     }
 }
 
 ====Usage Example====
 //Using a double scripted array as an adjacency matrix
 rowZero = new Array(0, 1000000, 1000000, 1000000, 5, 12);
 rowOne = new Array(15, 0, 9, 1000000, 1000000, 1000000);
 rowTwo = new Array(1000000, 1000000, 0, 5, 1000000, 1000000);
 rowThree = new Array(1000000, 2, 1000000, 0, 1000000, 1000000);
 rowFour = new Array(1000000, 1000000, 10, 1000000, 0, 4);
 rowFive = new Array(1000000, 1000000, 17, 20, 1000000, 0);
 
 ourMap = new Array(rowZero, rowOne, rowTwo, rowThree, rowFour, rowFive);
 
 var dijkstra = new Dijkstra(ourMap, 0, 1000000);
 dijkstra.findShortestPath();
 ====Done Usage Example====

Python

 import sys
 infinity = sys.maxint - 1
 
 class Vertex(object):
     """A vertex in a graph, using adjacency list.
 
     'edges' is a sequence or collection of tuples (edges), the first element of
     which is a name of a vertex and the second element is the distance to that vertex.
     'name' is a unique identifier for each vertex, like a city name, an integer, a tuple of coordinates..."""
 
     def __init__(self, name, edges):
         self.name = name
         self.edges = edges
 
 def ShortestPath(graph, source, dest):
     """Returns the shortest distance from source to dest and a list of traversed vertices, using Dijkstra's algorithm.
 
     Assumes the graph is connected."""
 
     distances = {}
     names = {}
     path = []
     for v in graph:
         distances[v.name] = infinity # Initialize the distances
         names[v.name] = v # Map the names to the vertices they represent
     distances[source.name] = 0 # The distance of the source to itself is 0
     dist_to_unknown = distances.copy() # Select the next vertex to explore from this dict
     last = source
     while last.name != dest.name:
         # Select the next vertex to explore, which is not yet fully explored and which 
         # minimizes the already-known distances.
         next = names[ min( [(v, k) for (k, v) in dist_to_unknown.iteritems()] )[1] ]
         for n, d in next.edges: # n is the name of an adjacent vertex, d is the distance to it
             distances[n] = min(distances[n], distances[next.name] + d)
             if n in dist_to_unknown:
                 dist_to_unknown[n] = distances[n]
         last = next
         if last.name in dist_to_unknown: # Delete the completely explored vertex
             path.append(last.name)
             del dist_to_unknown[next.name]
     return distances[dest.name], path

PHP

<?PHP
class Dijkstra {
 
	var $visited = array();
	var $distance = array();
	var $previousNode = array();
	var $startnode =null;
	var $map = array();
	var $infiniteDistance = 0;
	var $numberOfNodes = 0;
	var $bestPath = 0;
	var $matrixWidth = 0;
 
	function Dijkstra(&$ourMap, $infiniteDistance) {
		$this -> infiniteDistance = $infiniteDistance;
		$this -> map = &$ourMap;
		$this -> numberOfNodes = count($ourMap);
		$this -> bestPath = 0;
	}
 
	function findShortestPath($start,$to = null) {
		$this -> startnode = $start;
		for ($i=0;$i<$this -> numberOfNodes;$i++) {
			if ($i == $this -> startnode) {
				$this -> visited[$i] = true;
				$this -> distance[$i] = 0;
			} else {
				$this -> visited[$i] = false;
				$this -> distance[$i] = isset($this -> map[$this -> startnode][$i]) 
					? $this -> map[$this -> startnode][$i] 
					: $this -> infiniteDistance;
			}
			$this -> previousNode[$i] = $this -> startnode;
		}
 
		$maxTries = $this -> numberOfNodes;
		$tries = 0;
		while (in_array(false,$this -> visited,true) && $tries <= $maxTries) {			
			$this -> bestPath = $this->findBestPath($this->distance,array_keys($this -> visited,false,true));
			if($to !== null && $this -> bestPath === $to) {
				break;
			}
			$this -> updateDistanceAndPrevious($this -> bestPath);			
			$this -> visited[$this -> bestPath] = true;
			$tries++;
		}
	}
 
	function findBestPath($ourDistance, $ourNodesLeft) {
		$bestPath = $this -> infiniteDistance;
		$bestNode = 0;
		for ($i = 0,$m=count($ourNodesLeft); $i < $m; $i++) {
			if($ourDistance[$ourNodesLeft[$i]] < $bestPath) {
				$bestPath = $ourDistance[$ourNodesLeft[$i]];
				$bestNode = $ourNodesLeft[$i];
			}
		}
		return $bestNode;
	}
 
	function updateDistanceAndPrevious($obp) {		
		for ($i=0;$i<$this -> numberOfNodes;$i++) {
			if( 	(isset($this->map[$obp][$i])) 
			    &&	(!($this->map[$obp][$i] == $this->infiniteDistance) || ($this->map[$obp][$i] == 0 ))	
				&&	(($this->distance[$obp] + $this->map[$obp][$i]) < $this -> distance[$i])
			) 	
			{
					$this -> distance[$i] = $this -> distance[$obp] + $this -> map[$obp][$i];
					$this -> previousNode[$i] = $obp;
			}
		}
	}
 
	function printMap(&$map) {
		$placeholder = ' %' . strlen($this -> infiniteDistance) .'d';
		$foo = '';
		for($i=0,$im=count($map);$i<$im;$i++) {
			for ($k=0,$m=$im;$k<$m;$k++) {
				$foo.= sprintf($placeholder, isset($map[$i][$k]) ? $map[$i][$k] : $this -> infiniteDistance);
			}
			$foo.= "\n";
		}
		return $foo;
	}
 
	function getResults($to = null) {
		$ourShortestPath = array();
		$foo = '';
		for ($i = 0; $i < $this -> numberOfNodes; $i++) {
			if($to !== null && $to !== $i) {
				continue;
			}
			$ourShortestPath[$i] = array();
			$endNode = null;
			$currNode = $i;
			$ourShortestPath[$i][] = $i;
			while ($endNode === null || $endNode != $this -> startnode) {
				$ourShortestPath[$i][] = $this -> previousNode[$currNode];
				$endNode = $this -> previousNode[$currNode];
				$currNode = $this -> previousNode[$currNode];
			}
			$ourShortestPath[$i] = array_reverse($ourShortestPath[$i]);
			if ($to === null || $to === $i) {
			if($this -> distance[$i] >= $this -> infiniteDistance) {
				$foo .= sprintf("no route from %d to %d. \n",$this -> startnode,$i);
			} else {
				$foo .= sprintf('%d => %d = %d [%d]: (%s).'."\n" ,
						$this -> startnode,$i,$this -> distance[$i],
						count($ourShortestPath[$i]),
						implode('-',$ourShortestPath[$i]));
			}
			$foo .= str_repeat('-',20) . "\n";
				if ($to === $i) {
					break;
				}
			}
		}
		return $foo;
	}
} // end class 
?>

Usage Example

<?php
 
// I is the infinite distance.
define('I',1000);
 
// Size of the matrix
$matrixWidth = 20;
 
// $points is an array in the following format: (router1,router2,distance-between-them)
$points = array(
	array(0,1,4),
	array(0,2,I),
	array(1,2,5),
 	array(1,3,5),
	array(2,3,5),
	array(3,4,5),
	array(4,5,5),
	array(4,5,5),
	array(2,10,30),
	array(2,11,40),
	array(5,19,20),
	array(10,11,20),
	array(12,13,20),
);
 
$ourMap = array();
 
 
// Read in the points and push them into the map
 
for ($i=0,$m=count($points); $i<$m; $i++) {
	$x = $points[$i][0];
	$y = $points[$i][1];
	$c = $points[$i][2];
	$ourMap[$x][$y] = $c;
	$ourMap[$y][$x] = $c;
}
 
// ensure that the distance from a node to itself is always zero
// Purists may want to edit this bit out.
 
for ($i=0; $i < $matrixWidth; $i++) {
    for ($k=0; $k < $matrixWidth; $k++) {
        if ($i == $k) $ourMap[$i][$k] = 0;
    }
}
 
 
// initialize the algorithm class
$dijkstra = new Dijkstra($ourMap, I,$matrixWidth);
 
// $dijkstra->findShortestPath(0,13); to find only path from field 0 to field 13...
$dijkstra->findShortestPath(0); 
 
// Display the results
 
echo '<pre>';
echo "the map looks like:\n\n";
echo $dijkstra -> printMap($ourMap);
echo "\n\nthe shortest paths from point 0:\n";
echo $dijkstra -> getResults();
echo '</pre>';
 
?>

Visual Basic

    Option Explicit
 
    Const nodeCount As Integer = 9          'number of nodes - 1
    Type DijkEdge
        weight As Integer                   'distance from vertices that it is connected to
        destination As Integer              'name of vertice that it is connected to
    End Type
 
    Type Vertex
        connections(nodeCount) As DijkEdge  'hold information above for each connection
        numConnect As Integer               'number of connections - 1
        distance As Integer                 'distance from all other vertices
        isDead As Boolean                   'distance calculated
        name As Integer                     'name of vertice
    End Type
 
    Public Sub dijkstra_shortest_Path()
        Const infinity As Integer = 15000   'number that is larger than max distance
        Dim i As Integer                    'loop counter
        Dim j As Integer                    'loop counter
        Dim sourceP As Integer              'point to determine distance to from all nodes
        Dim inputData As String             'temp variable to ensure good data enterred
        Dim graph(nodeCount) As Vertex      'all inforamtion for each point (see Vertex declaration above)
        Dim nextP As Integer                'closest point that is not dead
        Dim min As Integer                  'distance of closest point not dead
        Dim outString As String             'string to display the output
        Dim goodSource As Boolean
 
        'user enters source point data and ensured that it is correct
        Do
            goodSource = True
            inputData = (InputBox("What is the source point: ", "Source Point between: 0 & " & nodeCount))
            If IsNumeric(inputData) Then
                sourceP = CInt(inputData)
                If sourceP > nodeCount Or sourceP < 0 Then
                    MsgBox "Source point must be between 0 & " & nodeCount & "."
                    goodSource = False
                End If
            Else
                MsgBox "Source point must be numeric and be between 0 & " & nodeCount & "."
                goodSource = False
            End If
        Loop While Not goodSource
        'get data so we can analyze the distances
        Call populateGraph(graph)
 
        'set default values to not dead and distances to infinity (unless distance is to itself)
        For i = 0 To nodeCount
            If graph(i).name = sourceP Then
                graph(i).distance = 0
                graph(i).isDead = False
            Else:
                graph(i).distance = infinity
                graph(i).isDead = False
            End If
        Next i
 
        For i = 0 To nodeCount
            min = infinity + 1
            'determine closest point that is not dead
            For j = 0 To nodeCount
                If Not graph(j).isDead And graph(j).distance < min Then
                    nextP = j
                    min = graph(j).distance
                End If
            Next j
            'calculate distances from the closest point & to all of its connections
            For j = 0 To graph(nextP).numConnect
                If graph(graph(nextP).connections(j).destination).distance > graph(nextP).distance + graph(nextP).connections(j).weight Then
                    graph(graph(nextP).connections(j).destination).distance = graph(nextP).distance + graph(nextP).connections(j).weight
                End If
            Next j
            'kill the value we just looked at so we can get the next point
            graph(nextP).isDead = True
        Next i
 
        'display the distance from the source point to all other points
        outString = ""
        For i = 0 To nodeCount
            outString = outString & "The distance between nodes " & sourceP & " and " & i & " is " & graph(i).distance & vbCrLf
        Next i
        MsgBox outString
    End Sub

Example Data for testing

    Private Sub populateGraph(vertexMatrix() As Vertex)
        'get data into graph matrix to determine distance from all points
        Dim i As Integer
        Dim j As Integer
 
        '0 connections
        vertexMatrix(0).name = 0
        vertexMatrix(0).numConnect = 3
        vertexMatrix(0).connections(0).destination = 1
        vertexMatrix(0).connections(1).destination = 2
        vertexMatrix(0).connections(2).destination = 6
        vertexMatrix(0).connections(3).destination = 7
        vertexMatrix(0).connections(0).weight = 10
        vertexMatrix(0).connections(1).weight = 15
        vertexMatrix(0).connections(2).weight = 30
        vertexMatrix(0).connections(3).weight = 50
 
        '1 connections
        vertexMatrix(1).name = 1
        vertexMatrix(1).numConnect = 3
        vertexMatrix(1).connections(0).destination = 0
        vertexMatrix(1).connections(1).destination = 3
        vertexMatrix(1).connections(2).destination = 4
        vertexMatrix(1).connections(3).destination = 9
        vertexMatrix(1).connections(0).weight = 10
        vertexMatrix(1).connections(1).weight = 16
        vertexMatrix(1).connections(2).weight = 5
        vertexMatrix(1).connections(3).weight = 40
 
        '2 connections
        vertexMatrix(2).name = 2
        vertexMatrix(2).numConnect = 3
        vertexMatrix(2).connections(0).destination = 0
        vertexMatrix(2).connections(1).destination = 7
        vertexMatrix(2).connections(2).destination = 8
        vertexMatrix(2).connections(3).destination = 9
        vertexMatrix(2).connections(0).weight = 15
        vertexMatrix(2).connections(1).weight = 33
        vertexMatrix(2).connections(2).weight = 18
        vertexMatrix(2).connections(3).weight = 60
 
        '3 connections
        vertexMatrix(3).name = 3
        vertexMatrix(3).numConnect = 1
        vertexMatrix(3).connections(0).destination = 1
        vertexMatrix(3).connections(1).destination = 4
        vertexMatrix(3).connections(0).weight = 16
        vertexMatrix(3).connections(1).weight = 22
 
        '4 connections
        vertexMatrix(4).name = 4
        vertexMatrix(4).numConnect = 2
        vertexMatrix(4).connections(0).destination = 1
        vertexMatrix(4).connections(1).destination = 3
        vertexMatrix(4).connections(2).destination = 5
        vertexMatrix(4).connections(0).weight = 5
        vertexMatrix(4).connections(1).weight = 22
        vertexMatrix(4).connections(2).weight = 30
 
        '5 connections
        vertexMatrix(5).name = 5
        vertexMatrix(5).numConnect = 0
        vertexMatrix(5).connections(0).destination = 4
        vertexMatrix(5).connections(0).weight = 30
 
        '6 connections
        vertexMatrix(6).name = 6
        vertexMatrix(6).numConnect = 1
        vertexMatrix(6).connections(0).destination = 0
        vertexMatrix(6).connections(1).destination = 7
        vertexMatrix(6).connections(0).weight = 30
        vertexMatrix(6).connections(1).weight = 40
 
        '7 connections
        vertexMatrix(7).name = 7
        vertexMatrix(7).numConnect = 3
        vertexMatrix(7).connections(0).destination = 0
        vertexMatrix(7).connections(1).destination = 2
        vertexMatrix(7).connections(2).destination = 8
        vertexMatrix(7).connections(3).destination = 6
        vertexMatrix(7).connections(0).weight = 50
        vertexMatrix(7).connections(1).weight = 33
        vertexMatrix(7).connections(2).weight = 3
        vertexMatrix(7).connections(3).weight = 40
 
        '8 connections
       vertexMatrix(8).name = 8
       vertexMatrix(8).numConnect = 1
       vertexMatrix(8).connections(0).destination = 2
       vertexMatrix(8).connections(1).destination = 7
       vertexMatrix(8).connections(0).weight = 18
       vertexMatrix(8).connections(1).weight = 3
 
        '9 connections
       vertexMatrix(9).name = 9
       vertexMatrix(9).numConnect = 1
       vertexMatrix(9).connections(0).destination = 1
       vertexMatrix(9).connections(1).destination = 2
       vertexMatrix(9).connections(0).weight = 40
       vertexMatrix(9).connections(1).weight = 60
    End Sub

Algorithmus von Dijkstra

Inhaltsverzeichnis

Algorithmus

Grundlegende Konzepte und Verwandtschaften

Berechnung eines Spannbaumes

Zeitkomplexität

Anwendungen

Siehe auch

Literatur

Weblinks

Literatur / Literature

Weblinks

Code

C

C++

Actionscript

Python

PHP

Usage Example

Visual Basic

Example Data for testing

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Mehr

Suche

Themen

Navigation

Werkzeuge

in Wikipedia